코딩을 공부하지 않아도 살면서 알고리즘에 대한 이야기를 많이 듣는다
예컨대 뉴스 기사 등에서 SNS 나 AI 에 대한 이야기를 할 때 늘 거론되기 때문이다
의미를 정확히 모르지만 문맥 내에서도 파악은 되었었다
오늘은 알고리즘에 대해서 명확하게 알아보고자한다
알고리즘(Algorithm)은 어떤 목적을 달성하거나 결과물을 만들어내기 위해 정의된 일련의 규칙이나 절차를 말한다
컴퓨터 과학에서 알고리즘은 특정 입력을 받아 출력 결과를 생성하는 유한한 단계로 이루어진 명령집합으로 정의한다
알고리즘의 주요 특징은 아래와 같다
알고리즘의 주요 특징
1. 명확성(Defintieness): 각 단계는 명확하고 모호하지 않아야 한다
2. 유한성(Finiteness): 알고리즘은 반드시 유한한 단계 안에 종료되어야 한다
3. 입력(Input): 알고리즘은 0개 이상의 입력을 받을 수 있다
4. 출력(Out): 알고리즘은 최소 1개 이상의 출력 결과를 생성해야 한다
5. 효율성(Efficiency): 알고리즘은 실행 시간과 자원 사용 측면에서 효율적이어야한다
알고리즘의 종류는 다양하다
따라서 직면한 상황에 따라 적절한 알고리즘을 선택해야한다
오메가(Ω) - 최상, 세타(θ) - 평균 측정 등 표기법과 기준으로 성능을 예측한다
시간복잡도와 공간복잡도가 위의 두 척도가 된다
시간 복잡도(Time Complexicity)란,
특정한 크기의 입력에 대하여 알고리즘의 수행 시간 분석, 알고리즘을 실행하여 종료할 때가지 걸리는 시간을 의미한다
간단하게 말하면, 알고리즘을 위해 팔요한 연산 횟수이다
공간 복잡도(Space Complexity)란,
특정한 크기의 입력에 대해 알고리즘의 메모리 사용량 분석, 알고리즘을 실행하여 종료할 때까지 필요한 기억장치의 크기를 말한다
메모리 용량에 대해서는 과거에 비해 컴퓨터 자체나 클라우딩 서비스 등으로 자유로워져서 잘 다루지 않는다고 한다
따라서 지금부터는 시간 복잡도에 초점을 맞춰 설명하고자한다
시간 복잡도를 표현하는 가장 보편적인 방법은 빅오 표기법(Big-O Notation)이다
빅오 표기법은 가장 최악의 경우를 생각하는 방법이다
따라서 불필요한 연산을 제거하여 알고리즘 분석을 쉽게 하기 위한 목적으로 사용된다
시간 복잡도는 수가 가장 작은 것이 연산 횟수가 적은 것을 나타내기 때문에 작은 수가 유리하다
아래는 시간복잡도를 단계별로 나타낸 것이다

시간복잡도 단계
O(1) < O(log n) < O(n) < O(n log n) < O(n^2)
O(1) - 상수 시간: 문제를 해결하는데 오직 한 단계만 처리함
O(log n) - 로그 시간: 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듦
O(n) - 직선적 시간: 문제를 해결하기 위한 단계의 수와 입력값 N 이 1 : 1 관계를 가짐
O(n log n) - 선형로그형: 문제를 해결하기 위한 단계의 숙 N*(log2N) 번 만큼의 수행시간을 가진다
O(n^2) - 2차 시간: 문제를 해결하기 위한 단계의 수는 입력값 N^2(N의 제곱)
이론적인 개념은 위와 같다
사실 이렇게 받아들이는 것 만으로 감을 잡기는 어려웠다
따라서 실제 자료구조에 따라 시간 복잡도가 달라지는지 알아보고 싶었다
아래 그림은 자료구조와 명령어 별 시간복잡도를 보여준다
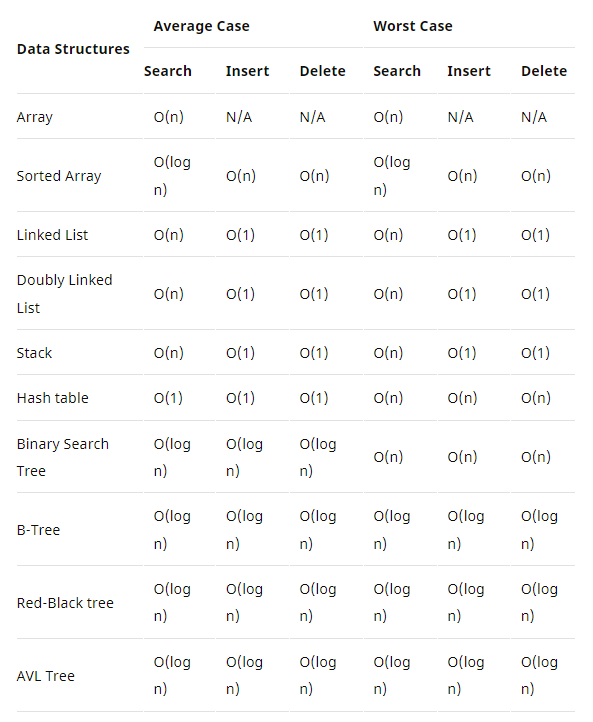
이렇게 표로 보니 자료구조마다 유리한 점과 불리한 점이 있음이 확연히 드러났다
그러나 실제로 속도를 체감할 일이 없다보니 나름대로의 실험을 하고 싶었다
아래는 LinkedList 와 ArrayList 객체를 생성한 후 두 객체의 알고리즘 수행 시간을 비교해보고자 짠 코드이다
ArrayList<Integer> arrayList = new ArrayList<>();
LinkedList<Integer> linkedList = new LinkedList<>();
long startTime = System.currentTimeMillis();
for (int i = 1; i < 1000000; i ++) {
arrayList.add((int) (Math.random() * 10));
}
long endTime = System.currentTimeMillis();
logger.log(Level.INFO, String.valueOf(endTime - startTime));
startTime = System.currentTimeMillis();
for (int i = 1; i < 1000000; i ++) {
linkedList.add((int) (Math.random() * 10));
}
endTime = System.currentTimeMillis();
logger.log(Level.INFO, String.valueOf(endTime - startTime));
startTime = System.currentTimeMillis();
for (int i = 0; i < 100000; i++) {
long num = (long) (Math.random() * 100000);
long targetIndex = num % 100000;
int flooredTargetIndex = (int)Math.floor(targetIndex);
arrayList.set(flooredTargetIndex, 1);
}
endTime = System.currentTimeMillis();
logger.log(Level.INFO, String.valueOf(endTime - startTime));
startTime = System.currentTimeMillis();
for (int i = 1; i < 100000; i += 2) {
long num = (long) (Math.random() * 10000);
long targetIndex = num % 10000;
int flooredTargetIndex = (int)Math.floor(targetIndex);
linkedList.set(flooredTargetIndex, 1);
}
endTime = System.currentTimeMillis();
logger.log(Level.INFO, String.valueOf(endTime - startTime));
실험 내용은 ArrayList 와 LinkedList 의 객체 추가 시간과 값을 찾아서 업데이트하는 시간을 비교하는 것이다
각 리스트마다 1 ~ 10 사이의 수를 1,000,000번 랜덤 생성해 추가하는 시간을 측정했다
그 후 각 리스트에 0부터 100,000 사이의 인덱스를 100,000 번 1로 바꾸는 시간을 측정했다
결과는 아래와 같았다
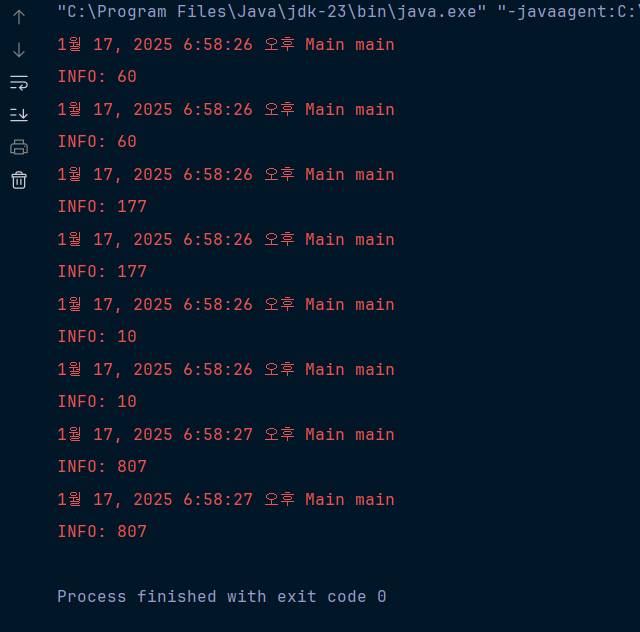
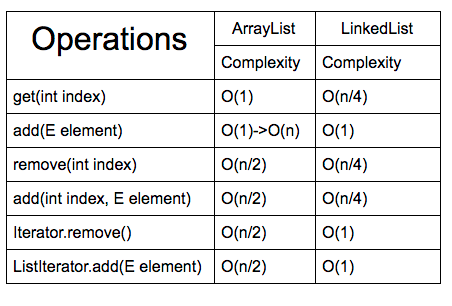
결과는 예상 밖이었다
LinkedList 가 삽입과 삭제 면에서 두드러지게 빠를 것이라고 예상했다
그러나 위 표와 같이 삽입의 면에서 add() 메서드는 LinkedList 와 ArrayList의 속도가 같았다
그래도 ArrayList 가 더 빠른 것은 놀라웠다
조금 더 찾아보니 LinkedList 는 remove() 메서드 면에서 매우 빠르다고 한다(ArrayList n/2, LinkedList n/4)
인덱스를 찾아 교체하는 작업에서는 ArrayList 가10, LinkedList 가 807 밀리초로 ArrayList 의 성능이 훨씬 좋았다
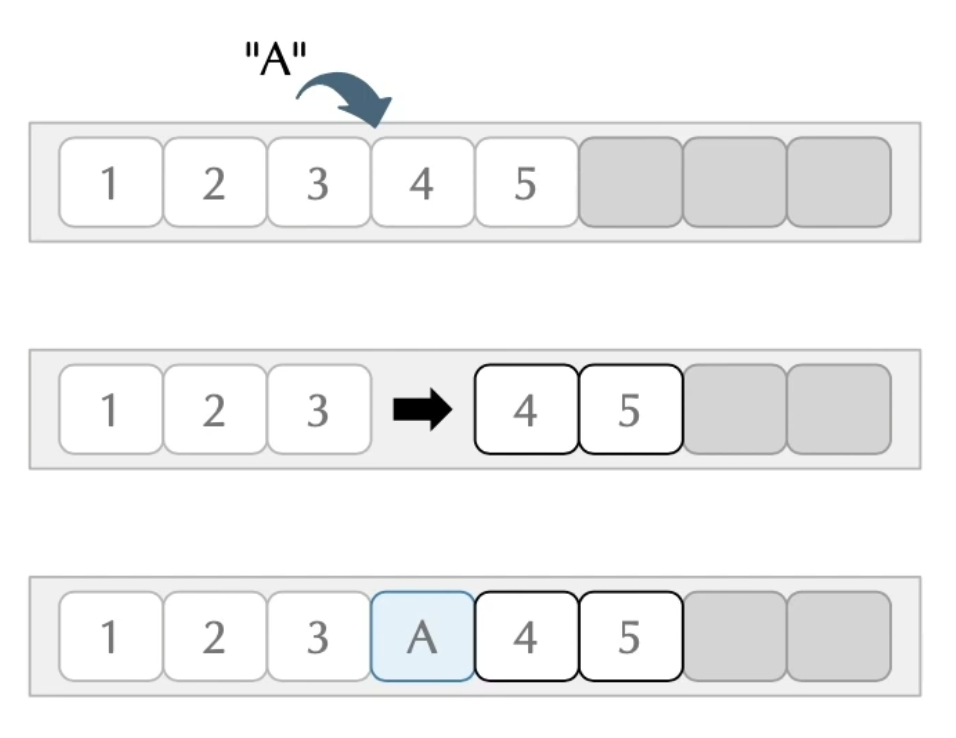
ArrayList의 삽입은 위 사진처럼 이루어진다
정해진 인덱스 값의 위치의 객체들을 하나씩 미루면서 삽입한다
아래는 ArrayList 의 add() 메소드 내부 코드이다
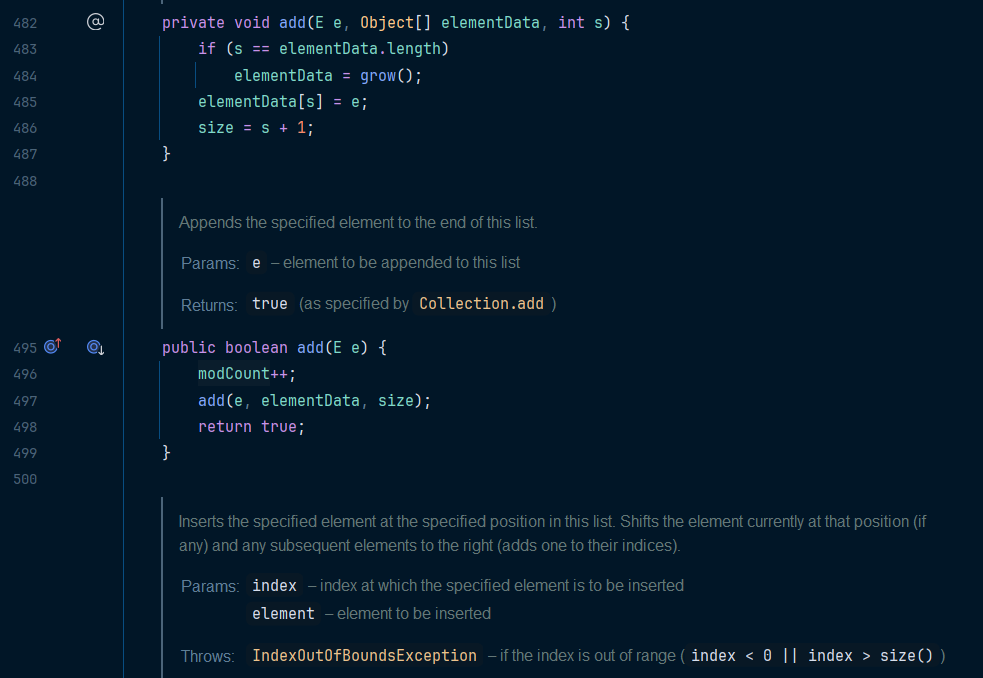
add() 의 매개변수를 추가해 저장하기만 할 줄 알았는데 내부적으로 add(요소, 요소배열, 요소크기) 메소드가 작동한다
위의 add() 메서드를 살펴보면 내부적으로 사용하도록 private 접근제어자로 제한한 것을 볼 수 있다
그리고 추가가 되기 때문에 배열의 크기가 추가되기 전 크기와 같을 떄 배열의 사이즈를 1 증가 시키고 값을 추가하는 것을 볼 수 있다
아래는 LinkedList 의 add() 메서드이다
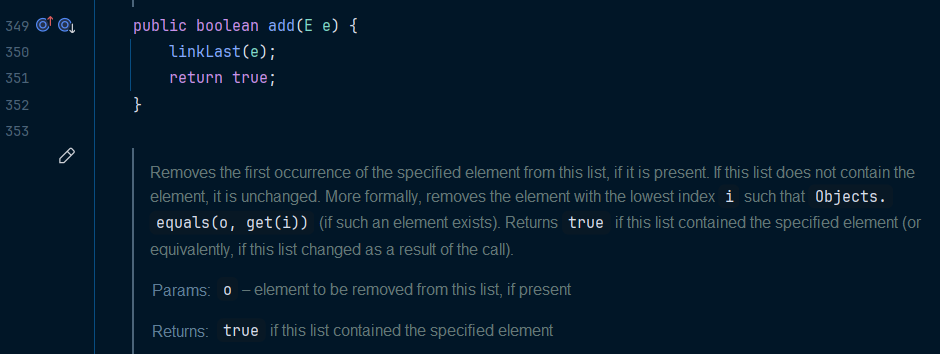
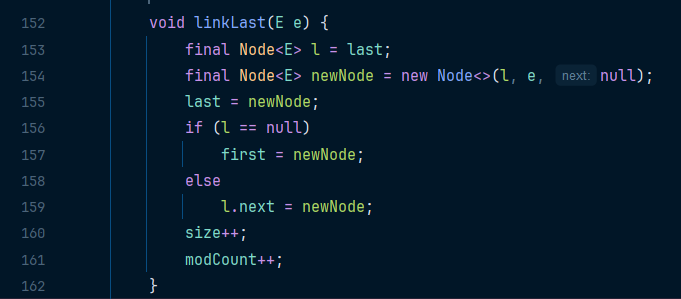
내부적으로 Node 를 생성하는 것을 알 수 있다
이때 Node의 생성자에는 3가지의 매개변수가 존재한다
각각 마지막 노드 주소, 요소의 값, 그리고 다음 노드 주소이다
노드를 생성하고 난 후에 last 변수 값을 현재 생성된 노드로 설정한다
그리고 마지막 노드 값이 없을 경우, 즉 노드가 존재하지 않을 경우 새롭게 생성된 노드를 첫노드로 설정한다
그 외에는 마지막 노드의 다음 노드로 생성된 노드로 설정한다
LinkedList 의 내부 코드를 보니까 값과 포인터로 이루어져있다는 추상적 설명이 조금 가시적으로 느껴졌다
작게 실험했던 메소드를 살펴보면 set() 메소드를 사용했고 성능차이가 났었다
그래서 set() 메소드의 내부구조도 비교해보려고 한다
아래는 ArrayList의 set() 메소드이다
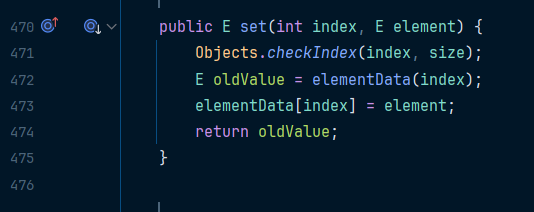
인덱스가 있는지 체크한 후 있을 경우 바로 인덱스 값을 업데이트해주는 것을 볼 수 있다
아래는 LinkedList의 set() 메소드이다
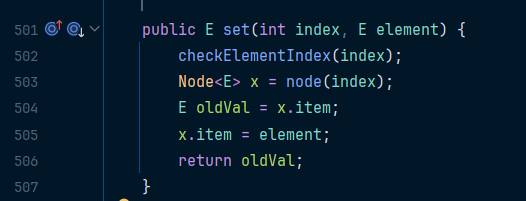
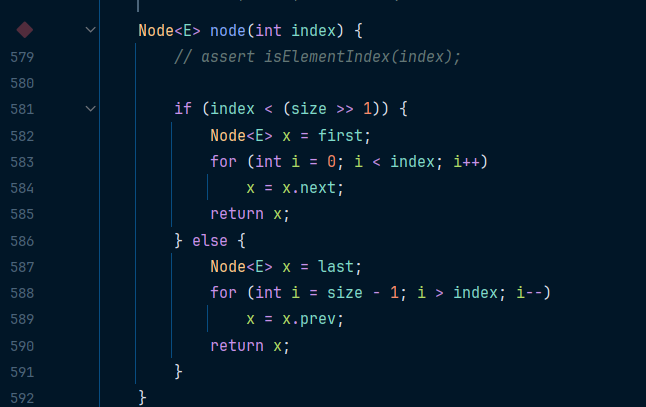
인덱스 존재 여부를 체크하고 node() 라는 메소드로 이어진다
이 메소드를 보면 내부적으로 for 문을 돌려(순회) 인덱스값의 노드를 반환한다
그리고 그 노드의 요소값을 바꾸려는 값으로 업데이트한다
이때 위의 알고리즘 개념을 사용하면 값체크, for문 돌기 등의 연산이 추가로 필요하다
따라서 시간복잡도가 올라가고, 많은 시간이 소요된다
알고리즘, 시간 복잡도, 자료구조 등 어렵고 추상적인 개념이기 때문에 이해하는 데 쉽지 않았다
하지만 오늘 이렇게 이해한 만큼 다음에 하게 될 공부가 조금 수월해질 것이라고 믿는다
차근차근 천천히 알아가자 화이팅 ~
'[Kotlin&Spring] 5기 내일배움캠프' 카테고리의 다른 글
| [Kotlin&Spring] 5기 로컬과 웹에서의 Cache (2) | 2025.01.21 |
|---|---|
| [Kotlin&Spring] 5기 API - REST API 중심으로 (0) | 2025.01.20 |
| [Kotlin&Spring] 5기 ArrayList 와 HashMap - Kiosk 과제 트러블슈팅 (0) | 2025.01.16 |
| [Kotlin&Spring] 5기 Abstract Class 와 Interface (1) | 2025.01.15 |
| [Kotlin&Spring] 5기 Java 부동소수점방식과 BigDecimal 타입 (0) | 2025.01.14 |



